「我最後一塊堅持不要的拼圖」之 「原來畫質是有差的」
| sya整理(2013.01.13最後更新) | Nikkor 70-200mm F2.8 | Nikkor 70-200mm F4 | Nikkor 28-300mm |
| MTF Chart(廣角端) |  |
 |
 |
| MTF Chart(望遠端) |  |
 |
 |
| 廣角端 | 中央:較佳 邊緣:較佳 |
ㄆㄨㄣ | |
| 望遠端 | 中央:F11後,畫質較佳 邊緣:較佳 |
中央:F4~F11,畫質較佳 | ㄆㄨㄣ |
| Sample Gallery | 點選 Mobile01上的評測 或 dpreview | 點選 Mobile01上的評測 | |
| 其他參考資料 | DPREVIEW介紹 | DPREVIEW介紹 | DPREVIEW介紹 |
| 最大光圈 | f/2.8 | f/4 | f/3.5~5.6 |
| 最小光圈 | f/22 | f/32 | f/22~38 |
| 最短對焦距離 | 1.4m | 1m | 0.5m |
| 鏡頭寬度 | 77mm | 77mm | 77mm |
| 直徑 x 長度 | 87 x 205.5 mm | 87 x 205.5 mm | 83 x 114.5 mm |
| 重量 | 1,540g | 850g | 800g |
| 影像穩定度 | 四級防手震 | 五級防手震 | 四級防手震 |
| Lens collar | 有 | 無 | 無 |
| 變形抑制 | 變形抑制佳 | 在望遠端變形較為嚴重 | 廣角端變形較為嚴重 |
| 暗角 | 不明顯 | 不明顯 | 廣角端暗角嚴重,望遠端也有輕微暗角 |
| 對焦速度 | TBC… | TBC… | TBC… |
| 價格(公司貨) | $72,000 | $39,000 | $26,800 |
從D80開始,一直以來我都是旅遊鏡的愛好者。但這次到虎山拍攝夜景,終於明顯的感受到鏡頭畫質上差異所帶來的差別。而且這畫質上的差異不是差一點點,而是非常非常的明顯!因此開始上網找一些資料,去了解這些鏡頭的解像力與範例圖片,來作為選擇的依據。順便來補一下在拍照上的基礎知識,要不然這樣胡亂拍了五、六年,似乎一些原理也都還不是很清楚。我發現我真是很喜歡做美勞,除了無聊的週末在家看一些投影片、算算國中數學外,還喜歡畫這些圖。真是很糟糕,我被污染了…..
從MTF Chart來看,70-200mm F2.8與F4在對比與解像力上的確是不相上下,甚至F4還可能超越F2.8;而散景的部分,從曲線上可以知道F2.8的散景應該會較為柔和、較為討喜。至於解像力的差異,在網路上有看到一種說法「肉眼對於對比的強烈程度較敏感,有時候會覺得對比明顯者比較銳利,但事實上那些鏡頭的解像力不一定比較高」。也就是說S10的對比值可能較S30的解像力對人眼有更大的視覺影響,甚至導致誤判。這點不知道是不是可以從上面Mobile01的連結來得到印證?從MTF圖上來看,70-200mm F4似乎在廣角與望遠端的解像力都較F2.8來的好,但從實際範例圖片來看,我個人是覺得F2.8這顆鏡皇:
1. 在成相品質上還是比較好
2. 在大太陽下不會有紫邊的情況發生 (這點倒是確定的)
關於MTF Chart,在網路上還有看到以下的心得:
※ 從MTF Chart來看的話,實線與虛線越接近,其散景較自然、好看,而不會呈撕裂狀。
※ 通常長焦鏡的 MTF 比廣角鏡的 MTF 要好。(但指的應該是解像力,而非散景的柔和度)
※ 大光圈與小光圈的MTF Chart越接近,代表鏡頭的品質越好。
從上面提到的散景,順便的到網路上瞭解了一下景深的原理與計算方式,跟大家分享在下面。
景深與對焦
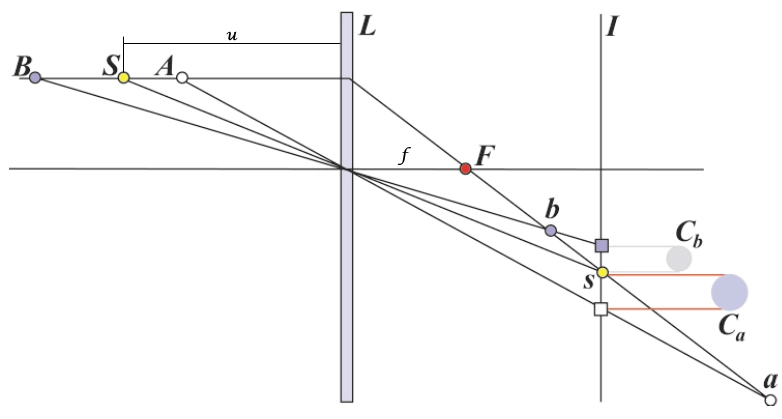
↑ 對焦說明圖 (F:焦點。f:焦距。S:對焦點。L:鏡片。I:成相位置(感光元件))
最大可接受模糊圓直徑(Diameter of the maximum permissible circle of confusion, CoC),Leica的工程師初期在135底片(全幅)上,透過經驗定義了「當模糊圓的直徑≦1/30mm時,人眼就無法分辨出這究竟是一個點還是一個圓」,因此就將這個大小稱做是最大可接受的模糊圓直徑。也就是說,在這個情況下,我們會把它看成是準焦的情況。之後,國際上也接受了這樣的觀念,並隨著技術的進步,且對焦點不斷的精確下,目前廣泛的CoC定義如下:
CoC = 底片的對角線長(mm) / 1500
下面找了一些目前常見的感光元件大小給大家參考:
全幅:36×24mm
APS-C:25.1×16.7mm (仍依相機不同而不同)
4/3:18×13.5mm
景深(Depth of Field),接續上面的CoC概念,所謂的景深就是CoC的前後緣的範圍,以上面那個圖來舉例的話,也就是最大可接受的Cb的上限與最大可接受的Ca的下限。換成公式:
景深 = 景深後緣 – 景深前緣

在上面的公式中,參數的說明如下:
u:對焦距離
f:焦距
N:光圈值
C:CoC
在公式上,我另外加了一些簡單的紅色說明,因此可以清楚的看到,影響景深最大的最大因素,主要就是對焦的距離。從公式上來看,可以得知這個景深會與光圈值、CoC、對焦距離的平方成正比,而與焦距的平方成反比。至於這個景深前緣與景深後緣的公式是怎麼推算出來的,我倒是沒有再去深究了。
泛焦距離(Hyperfocal distance),所指的其實就是指「最大景深」的發生時機,透過這樣的方式,可以達到極速對焦的目的,且拍出來的景物將大部分是清晰的。說極速對焦,其實就是不用對焦,因此景物在進入設定的範圍後即可拍攝,且盡量保持畫面的清晰。從景深後緣的公式來看,當分母的部分趨近於0的時候,就會有最大的景深。因此便可以推出下面的結果:

再將上面的這個結果帶回景深前緣的公式,便可以得到在條件下,景深的前緣與後緣大約會是下面的這個關係:

至於詳細的公式計算,我就沒有繼續找下去了。如果你有興趣的話,可以繼續到 這裡 找找詳細的公式推演。總之,從上面的公式個以約略的推知,當泛焦的情況成立時,景深的前緣大約是對焦距離的1/2,景深的後緣則當然是無限遠處。平常的話,可以利用國外的這個「線上景深計算器」網站,來計算看看泛焦的條件大約是在什麼情況下成立。以我的相機Nikon D700來說,當使用24mm的焦段時,若對焦物體的距離為2m。則當光圈F/9.5時,景深的前緣在1.01m、景深的後緣在95.8m;如果當光圈縮到F/10時,景深的前緣在0.98m、景深的後緣則在無限遠處。因此也就是說,如果在24mm焦段、光圈F10時,關閉相機上的自動對焦,將對焦環旋轉至2的地方後,就能夠享受泛焦帶來免對焦的清晰畫面。當然這個清晰的景深畫面範圍就界在0.98m~無限遠處。
最近對焦距離 與 放大倍率 的關係
最大放大倍率表示圖像感應器上成像的被攝體的最大尺寸。從上面的70-200 F2.8與F4兩顆鏡頭可以看到,同樣在200mm焦段下,F4的鏡頭可以獲得更大的放大倍率。這對我這個攝影幼幼班的人來說,剛看到這個結果真是讓我狐疑,覺得怎麼可能相同焦段下,拍出來的結果會不一樣呢?
原來照片的放大倍率不完全由焦段決定,如果找個比較簡單且好想像的例子,如果有A、B兩個鏡頭同樣都有100mm的焦段,A鏡頭最近的對焦距離為30cm,B鏡頭最近的對離為100cm。可以很輕易的想像A鏡頭獲得的放大率自然會比B鏡頭來得大。因此在物理特性上,望遠端當然也有相同的情況。因此一般有較近對焦距離的鏡頭,拍攝出來的影像在相同的焦段下,可以獲得較大的影像放大率。
所以很直觀的,定焦鏡頭在最近對焦距離拍攝的放大倍率為最大;如果是變焦鏡頭,當變焦鏡頭在望遠端時才能達到其最大放大倍率。而這個所謂的最大放大倍率,指的就是實物在感光元件上的成像大小。舉例來說,如果一個2cm直徑的錢幣,在感光元件上的成像大小為1cm,則放倍率就是0.5倍。最大放大倍率在0.5倍以上的鏡頭,一般就被稱為微距鏡頭。
【全幅機的優點?】
- 畫質 –
TBC… - 高ISO品質 –
CCD(CMOS)是由許多的單一感光體組成,多少像素就是有多少個感光體。其他關於高ISO與雜訊的討論,可以參考ptt上的 這篇文章。 - 較淺景深 –
TBC…
【星芒】
「星芒效果」屬於光線繞射的現象,一般將鏡頭光圈縮小,就容易拍出這樣的畫面。「星芒效果」的產生有幾個必要的因素:
A. 縮小光圈。
B. 場景之中,有強烈的點光源。
C. 點光源射入鏡頭後,產生繞射現象。
星芒效果的形狀和光圈的葉片設計有關,偶數光圈葉片,星芒數與葉片相同,奇數光圈葉片,星芒為葉片數兩倍。小光圈星芒現象會更明顯,因為更接近狹縫。
影響的因素:
- 光圈 – 光圈越小、星芒的長度越長
- ISO?
- 解像力 – 似乎無影響
至於寫了這麼多,到底要買哪一顆鏡頭?目前初步應該是會選擇70-200mm F2.8。一方面在畫質、最大光圈、散景等方面都有較高呈現,且也比較保值。看來,一直喜歡且衷情旅遊鏡的我,堅持了半天,最後「可能」還是會補滿最後的一張拼圖。總之,有天分的人靠構圖,有手段的人靠修圖,什麼都不太行的,只能傾家蕩產,用錢來換得一些些心靈上的平靜 @@ 阿彌陀佛…
結果最後還是留用旅遊鏡了,其他的,等改天樂透中了再說吧 😀
參考資料








